Incommensurable IcosahedraThe cuboctahedron and icosahedron, if spun around axes connecting opposite vertices, face centers, and mid-edges, generate spherical networks of 25 and 31 great circles respectively. These two great circle networks are described in terms of their surface and central angles, which Synergetics exhaustively tabulates. Crystal symmetries derive from the cuboctahedron's great circle set, while the quasi-crystalline, five-fold symmetries derive from the icosahedron's. When the two sets of symmetries are superimposed, we get what Fuller called the "Omni-rational Control Matrix" that may be used "for all topological, trigonometric, physical and chemical accounting." (2:901.19) The relationship between the volumes of the cuboctahedron (20) and icosahedron (18.51...), both of prime vector edge length and ratioed to the unit-volume tetrahedron, is incommensurable. Traditional text book demonstrations of incommensurability show that the edge of a square cannot be expressed as a rational fraction of its diagonal. But synergetics is typically volumetric in its presentation of such generalities. Whereas Euclidean geometry would confine itself to a plane, synergetics uses the jitterbug transformation. As a cuboctahedron - known as the vector equilibrium (VE) in synergetics [13] - twist-contracts into an icosahedron, its six square diagonals, each 2 in length, become unit edges (2:987.053). The Euclidean planar demonstration is implicit, but so is the transformation of the network of 25 into the network of 31 great circles, a transformation between symmetry groups. The discomfort experienced by Pythagoreans about the irrationality of root2 and modern uneasiness about "bizarre" quasicrystals are thereby shown to be intimately related: "VE:icosa = root2:2 = root2:1" (2:987.054). Another consistently recurrent number, phi, a hallmark of five-fold structuring, is also present in this transformation. The icosahedron's opposite edges pair up to form 15 golden rectangles, with longer sides of phi times the icosahedron's edge. |
 |
| In his contemplative little book, Science and Creation, John Polkinghorne, an Oxford physicist turned Anglican priest, writes about the phenomenon of chaos: "somewhere in between the fundamental physics of the very large and the very small - lying in fact at about the geometric mean of their length scales - is the world of everyday... However symmetric and orderly these extreme worlds may be, the world of everyday... seems much more untidy."[14] | 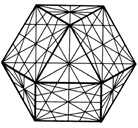 |
| Fuller calls this apparently disorderly world between extremes of scale "medio phase" (2:987.061) and attributes its chaotic nature to "the eternal war of incommensurability" regeneratively waged between the two great circle symmetry sets, the crystalline and the quasi-crystalline. "The self-regeneration of... beginningless and endless Scenario Universe inherently requires in pure principle an eternal incommensurability of - at minimum two - overall symmetrical and concentric system intertransformative behaviors and characteristic phases." (2:987.044) | |
| Crystallographer N.Y. Belov, writing in 1962, well before quasi-crystals were discovered, connected fivefold symmetry with the emergence of life itself: "It would appear that for small organisms the fivefold axis represents a distinctive instrument in their struggle for existence, acting as insurance against petrifaction, against crystallization, in which the first step would be their 'capture' by the lattice." And so the virus comes to symbolize the fragile concept of life itself, its icosahedral capsid marking the threshold between living and nonliving. "The supposed location of the threshold between animate and inanimate was methodically narrowed down by experimental science until it was confined specifically within the domain of virology" writes Fuller, in his introduction to Synergetics 2. |  |
| In A.L. Mackay's article "Lucretius: Atoms and Opinions" (Symmetry, 1:1, 1990), Belov's insight appears in the wider context of a meditation about the nature of language itself. Language is really not outside the phenomena it observes and as its descriptions of living and nonliving chemistries interpenetrate, it appears increasingly to take on the qualities of both. No physical threshold between living and nonliving really exists. "The possibility of its existence vanished because the supposedly unique physical qualities of both animate and inanimate have persisted right across yesterday's supposed threshold in both directions to permeate one another's - previously perceived to be exclusive - domains." | 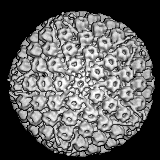 |
| Perhaps the occurrence of life is neither predicted nor explained by physics and chemistry in part because the very meaning of "alive" is always being regeneratively recomputed within the chaotic context of our everyday world. Language itself is "death defying" in the sense of "escaping 'capture' by the lattice" (or any omnirational, closed System) - the eternal war of incommensurability produces "eternal disquietude" in our thinking (987.058). "The invention of the game of limited and terminal local awareness that we call 'life' is in contradistinction to the concept of eternally total cosmic knowledge... whose totality of comprehensive comprehension would... result in the eternally timeless, sublime 0 = 0 equation of absolute perfection." (2:311.15) | |