Synergetica2


A Case of Deja Vu The recent spate of articles about buckminsterfullerene (Bf), named for "the inventor of the geodesic dome," is reminiscent of what happened in the 1960s when x-ray crystallographers Donald Casper and Aron Klug discovered the icosahedral shape of many of the viruses. "The protein outside the coat, far from being a 'bag,' is a beautifully constructed geometrical figure... many of which are like the architecturally famous domes of Buckminster Fuller" wrote Dean Fraser in his Viruses and Molecular Biology (Macmillan, 1967). Such references were typical. As Fuller recounts in Utopia or Oblivion (p. 104): "The virologist discovered the proliferation of my geodesic structures, which had emerged from structuring aspects of my energetic geometry studies..."
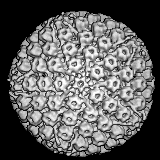The deeper connection between virology and synergetics is only hinted at by this micro-macro structural analogy however. For Fuller, the domes were simply artifacts that had "emerged" from his geometric investigations. "In 1957 Klug asked if I could identify the geodesiclike protein shell of the polio virus. I was able to give him the mathematical explanation of the structuring."
In Critical Path, Fuller records his contribution in the appended chronology under the year 1963: "World Congress of Virologists meeting Cold Spring Harbor, Long Island, N.Y., announce comprehensive discovery of protein shells of viruses, which they publicly acknowledge (featured, front page, New York Herald Tribune) as having been anticipated by RBF's formula of frequency to the second power of 10 plus 2." This expression 10F²+2 is what Fuller intended for use as a bridge to synergetics. Those who traced this formula from its front page mention in the newspaper to its origin in synergetics would come across its more general form: 2PF²+2, an expression at the heart of Fuller's investigations into sphere packings.
By setting P=5 in the expression 2PF²+2, the number of spheres in each successive layer of the cuboctahedron may be derived. F stands for "frequency" and is the number of intervals between spheres along any edge of the cuboctahedron or, alternatively, is the number of intervals along any radius between a corner sphere and the central one. In a virus, the RNA-protecting shell or capsid is made from sub-units called capsomeres. By taking F as the number of between-capsomere intervals, and using 10F²+2 on capsid "shell frequencies" of 1,2,3,4,5 and 6, we obtain corresponding counts of 12, 42, 92, 162, 252 and 812 capsomeres. "All of these numbers are in fact found in actual viruses, 12 for certain bacteriophages, 42 for wart viruses, 92 for reovirus, 162 for herpesvirus, 252 for adenovirus and 812 for a virus attacking crane-flies (Tipula or daddy-long-legs)" - The Natural History of Viruses by C.H. Andrews (W.W. Norton R Co., 1967).
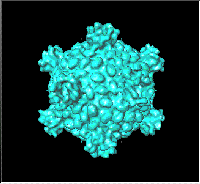
X-ray diffraction patterns showed these viruses to have icosahedral symmetry. How does the sphere packing formula derived for the cuboctahedron manage to predict the number of spheres in an icosahedrally shaped capsid? Again, Fuller hoped that his audience of virologists would be led by this question to his jitterbug transformation. The jitterbug motion, a combination of rotation and contraction, smoothly transforms the cuboctahedron into an icosahedron and vice versa. More generally, the jitterbug transformation serves as a unifying motion relating 4- and 5-fold symmetric polyhedra.
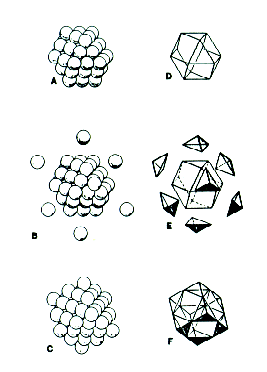
When applied to shells of closest packed spheres, the jitterbug transformation turns the cuboctahedral shell into an inherently non-nucleated one. The icosahedral arrangement is essentially hollow. It does not have room for concentric shells to be formed by closest packing - unless we allow the spheres to deform. Chemists have been able to generate icosahedral clusters of atoms by forcing xenon gas through a nozzle at high pressure. The xenon clusters, which spontaneously form as the gas cools, consist of concentric icosahedral shells - named Mackay shells after crystallographer Alan Mackay. The total number of atoms in such clusters is expressed using the familiar synergetics formula: N = 1 +SIGMA(10F²+ 2) Or, alternatively, one may derive:[2] N = (10/3)F³+ 5F²+(11/3)F + 1 This icosahedral cluster growth pattern cannot be maintained indefinitely out to any frequency however. At some point, it jitterbugs to release pent-up stress and relaxes into alignment with the isomatrix to become a stable crystal. As Dr. Bjornholm of the Niels Bohr Institute at the University of Copenhagen puts it: "The point is that hard spheres cannot really be packed into the icosahedron... The spheres have to be soft... As a result a strain builds up in the cluster and at some stage it becomes favourable to release the strain through a rearrangement of the atoms leading to the familiar cuboctahedral structure of the macroscopic crystal."[3] The jitterbug transformation has been discovered in nature. Spheres may be closest packed concentrically and omnisymmetrically to form shapes other than the cuboctahedron. Fuller discovered that by changing the value of P in his expression 2PF²+2, he was able to accommodate sphere packings which conformed to the external contours of other "primary systems." A tetrahedral packing is generated when P=l, an octahedral one when P=2, and a cubic packing when P=3.
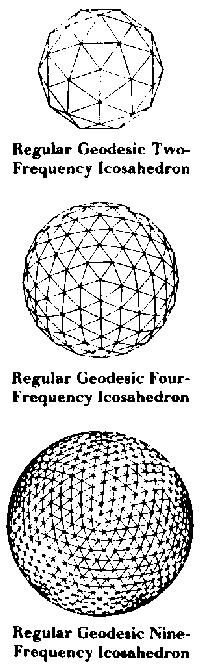When P=2, for example, the expression becomes 4F²+2, and gives the sphere populations in an octahedron's successive layers. Six spheres form an octahedron centered around a void while 18 build around a nuclear sphere to form a 2-frequency octahedron and so on. 6F²+2 describes the two packing arrangements which define a cube of any frequency: the body-centered cubic (bcp) and the one generated by tangent spheres inscribed in XYZ cubes.[4] These packings are not necessarily nucleated however (the tetrahedron acquires its first nucleus at frequency 4), nor is the cube as densely packed as the isomatrix will allow at some frequencies. The formation of nucleated densest packings of various shapes, excluding the inherently non-nucleated 5-fold symmetric polyhedra, is another, related topic which Fuller investigates in Synergetics and Synergetics 2 .[5] Fuller hoped that these investigations would prove useful in chemistry, where the arrangement of protons and neutrons in atomic nuclei might be modeled by sphere packings of various shapes.
Contrary to Fuller's hopes, however, 10F²+2 did not go down in history as a special case of 2PF²+2. It was instead subsumed by another expression. Casper and Klug found that Fuller's 10F²+2 did not account for all of the capsomere counts they were getting. They needed to accommodate the so-called "skew" cases corresponding to what later came to be known as Class III geodesic structures. In such cases, the rows of capsomeres are not parallel to the edges of an icosahedron but cross them at an angle. Their new expression was 10T²+2, where T=b²+bc+c². Casper and Klug's expression reduces to Fuller's when c=0.
We can suppose that Fuller's input helped Casper and Klug to derive their expression but, once published, it was incorporated into the literature in a way that did not link to Fuller. In his Virus Macromolecules and Geodesic Domes (1967), for example, H.S.M. Coxeter traced the newly emerging classification scheme for geodesic structures to mathematician Michael Goldberg's paper, A Class of Multi-Symmetric Polyhedra which appeared in 1937 (Tohoku Mathematics Journal, 43, 104 -108).	Virus Images Fullerenes Geodesic Spheres Sphere Packing
Coxeter rather patronizingly implied that Fuller-the-architect might learn something from a real mathematician: "Summarizing our conclusions, we may say that Goldberg's classification of 'multi-symmetric' polyhedra yields a convenient classification of possible shapes for virus macro-molecules and geodesic domes. The possibility b <> c may perhaps inspire Fuller to make new domes which, like pineapples and helices, have no planes of symmetry."[6] The fact that 10F²+2 also had another parent expression in synergetics, also more general but describing sphere packings rather than classes of geodesic structuring, was left out of this and subsequent accounts.[7]
Synergetics was most likely ignored during this period because it was as yet only available in fragments. By the mid-1980s, when articles about buckminsterfullerene began to proliferate, the situation had changed: Synergetics and Synergetics 2 had appeared, in 1975 and 1979 respectively. Now scientists could discover what Fuller was up to in his "energetic geometry studies" as they could not so easily during the virus scenario. The synergetics formula 10F²+2 may be modified to 20F²/3 (where F is a multiple of 3) to give the number of carbon atoms in a few of the fullerenes - those derived by removing nodes from the variable frequency icosasphere. C₆₀ (buckminsterfullerene) and some of the hypothesized "giant fullerenes" such as C₂₄₀, C₅₄₀ and C₉₆₀ are of this type. Many other permutations of hexagons and pentagons are possible however, as evidenced by the recently isolated C₇₆, in which the hexagons appear in a surprising helical pattern.[8]
In all of these structures, however, the number of pentagons is always 12, a fact which intrigued the virologists: "It should be noticed that the subunits are not identically located: most of them are surrounded by six others, but those at the corners of the icosahedron have five neighbors. Recent work shows that the protein subunits at these vertices of adenovirus are both serologically and morphologically different from the rest." (Fraser, 1967, pg. 53). This same spherical pattern of 12 pentagons and a variable number of hexagons occurs in another biological structure known as a "coated vesicle," which has an external lattice analogous to the viral capsid, known as clathrin. As mathematician Ian Stewart points out in Circularly covering clatharin (Nature, Vol 351, 9 May '91, pg. 103), the hexapent cage illustrates the optimal solution to the problem of how to cover a sphere with the least number of partially overlapping circles of the same radius. Mathematicians had hitherto missed this optimum fullerene-like solution. "Not for the first time, nature has beaten them at their own game" writes Stewart.
Sections: 1 2 3 4 5 6 7

A Case of Deja Vu