Using Polyhedra to Teach OOP
and Coordinate Geometry Concepts
Chapter 4:
Scaling and Translation
by Kirby Urner
First posted: Oct 29, 1998
Last modified: Nov 23, 1998
To scale a shape is to change its size. If the scale factor is greater than 1, the shape will grow. A scale factor value less than 1, but still positive, will cause it to shrink.
Internally, the scale() method in our polyhedron class passes a scale factor to oMatrixOps, where it gets used as a multiplier against all coordinates in the shape's Points table.
Additionally, to scale a shape is to changes its volume by a third power of the scale factor.
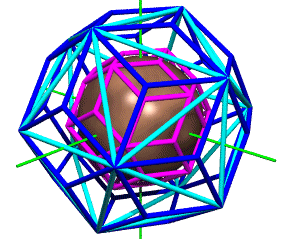
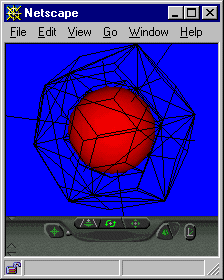
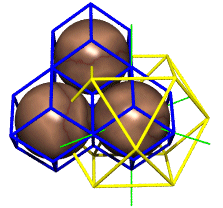
Our subclassed polyhedra all start with some defined shapevolume property, which gets multiplied by scalefactor^3 in the scale() method. The large blue 30-faced rhombic triacontahedron in the above figure has a body- to face-center radius of phi (about 1.618) and a volume of about 21.21. The inscribed 30-edged icosahedron (cyan) is a little smaller, weighing in at about 18.51:
define class icosahedron as polyhedron
shapeid = "I1"
snapshot = "I1points"
shapevolume = 18.51229586821915
shapecolor = "Cyan"
enddefine
The smaller rhombic triacontahedron (magenta), shrink-wrapped around a unit-radius sphere, has a volume of precisely 5 -- a result of internalized scaling properties designed for this purpose. Its body- to face-center radius is a hair less than the sphere's:
define class rhtriac as polyhedron
shapeid = "RT1"
snapshot = "RT1points"
shapevolume = 20 * (9/8)^0.5 && 20 * (synergetics constant)^3
emodfactor = 2/(1+5^.5) && 1/phi
tmodfactor = ((2^.5 * (2 + 5^.5))/6)^(1/3) && E-mod -> T-mod Rh Triac
shapecolor = "Magenta"
enddefine
The script below invokes these internal scale factors to generate the VRML view at right. This script is essentially the same as the one used to create the Povray script behind the above ray tracing, except in this case the WriteVRML subclass of WritePoly was used, instead of the WritePov subclass: