The original version of the essay below was first published to geometry-research at the Swarthmore Math Forum in April of 1998.
Beyond Flatland:
Geometry for the 21st Century
by Kirby UrnerFirst posted: April 22, 1998
Last modified: October 29, 1998
PART I: Pascal's Tetrahedron
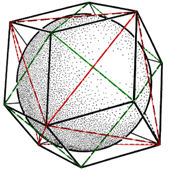
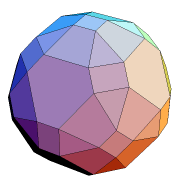
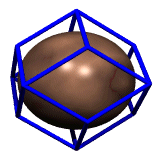
Agglomerating equi-radiused spheres outwardly from a central sphere in concentric cuboctahedral layers gives an isotropic Barlow packing more commonly known as the face-centered cubic or fcc. The packing subsumes the tetrahedral arrangement used to stack cannon balls, called the 'brass monkey' by some in USA civil war days, and commonly used for fruit-stacking in grocery stores. The nuclear sphere, plus layers out to one of the cuboctahedron's 8 trianglar facets, defines a tetrahedral packing.
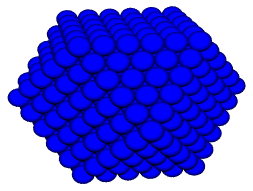
This packing is the volumetric analog of a triangulated peg board,
sometimes used as in the game of pachinko to vector falling balls,
with Pascal's triangle describing 'by how many paths' a given peg
might be reached, with 'how many' = 'the likelihood of ending up
somewhere' -- turns out to be a Gaussian distribution or
bell-shaped curve.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
By the same token, a tetrahedral packing, with an apexial entry point and fall-pattern with 3 choices per peg, to the base corners of a tet, defines "Pascal's Tetrahedron" of countable pathways, again with a kind of peak-shaped statistical outcome.
1 1 1 1 1
1 1 2 2 3 3 4 4
1 2 1 3 6 3 6 12 6
1 3 3 1 4 12 12 4
1 4 6 4 1
Pascal's Tetrahedron also describes the structure of diamond crystals, where the carbon atoms arrange in stacked tetrahedra.
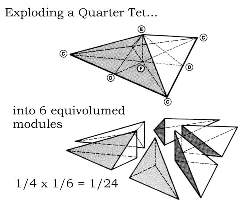
Another feature of the fcc pegboard is the fact that any four pegs not in the same plane define a tetrahedron of whole number volume, relative to a unit tetrahedron defined by four close-packed fcc spheres. This is true for skew as well as regular tetrahedra.
If the spheres have unit radius, then each sphere center is distance 2 from 12 surrounding centers, but this 2 also = 1 interval or 1 diameter, so the unit volume tetrahedron is likewise a model of 1x1x1 or 1^3, measuring in intervals.