Using Polyhedra to Teach OOP
and Coordinate Geometry Concepts
Chapter 2:
Sharing the Stage
by Kirby Urner
First posted: Oct 26, 1998
Last modified: Oct 29, 1998
In this demonstration we implement a somewhat more elaborate object-oriented model of a scene involving multiple polyhedra, drawing from the experienced gained in Chapter 1. Our two major enchancements have to do with allowing multiple polyhedra to maintain their independence, while appearing together.
If a tetrahedron rotates
around its X-axis by 90 degrees, this will not affect any other
polyhedra currently defined -- because every polyhedron object has
its own compartmented data tables.
oIcosa = createobject("icosahedron")
oTetra1 = createobject("tetrahedron")
oTetra2 = createobject("tetrahedron")
oIcosa.shapecolor="Cyan"
oTetra1.shapecolor="Orange"
oTetra2.shapecolor="Black"
oTetra2.rotate("X",90)
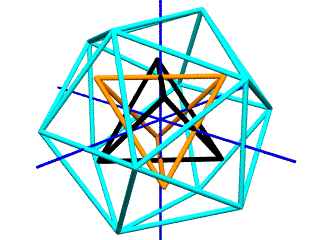
However, when we're ready to display our "actors", we want them to all share the same stage, to juxtapose and interpenetrate. This is accomplished by having all objects share a single "display server" which writes instructions to a single, shared Povray script (an ASCII text file).
This latter regime marks a departure from Chapter 1, wherein the oWritePOV object was added internally to the Polyhedron class. The former design caused a POV file to be initialized for each shape object. In the new design, oWritePOV floats in object space as a single shared resource.
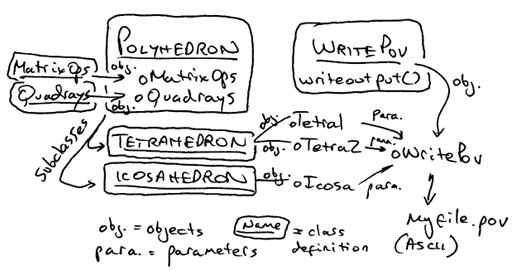
When we wish to write out a particular polyhedron for display, we pass a pointer to its object as a parameter, which in turn allows the writeoutput() method to locate and open the corresponding data tables unique to that object, and close them when done. The POV file itself gets initialized once, when oWritePOV is created, and all polyhedra write to this same output file (myfile.pov being the default name).
oWritePOV = createobject("WritePOV")
oWritePOV.axcolor = "Blue"
oWritePOV.makeaxes() && draw blue xyz axes
oWritepov.writeoutput(oIcosa) && objects passed by reference
oWritepov.writeoutput(oTetra1)
oWritepov.writeoutput(oTetra2)
Note the use of standard query language (SQL) to retrieve local Points and Edges tables from the archival tables. The shapes archive (shapes.dbf) inventories edges as vertex pairs (id1 and id2). It stores edges for lots of polyhedra, distinguishing them by shapeid. So the first SQL expression filters on this.shapeid, a corresponding property of the Polyhedron class, with its value preset by each subclass definition. For example, "T1" is the value of shapeid for the Tetrahedron subclass, and "I1" for the Icosahedron.
this.objedges = sys(3) && unique filename
select * from (this.edgearch) ed ;
where this.shapeid = ed.shapeid ;
into dbf (this.objedges)
The Points table gets defined using slightly more complicated logic. Now that an Edges table has been created, we want all the points mentioned in that Edges table, i.e. we need every unique (SQL "distinct") point listed in either the id1 or id2 column:
* create local (writable) Points table (alias points)
this.objpoints = sys(3) && unique filename
if this.baseformat = "xyz"
select distinct lib.pointid, xcoord, ycoord, zcoord ;
from (this.pointarch) lib, (this.objedges) ed ;
where (ed.id1=lib.pointid or ed.id2=lib.pointid) ;
into dbf (this.objpoints)
endif
Another twist has to do with a quirk of history. We inherited some archival Edges and Points tables as legacy data from another project. However, the Points table did not use xyz 3-tuples to record coordinate addresses, but a more exotic 4-tuple format known as the quadray format. For this reason, a Quadrays object (oQuadrays) is added to our polyhedron class, and its quad2xyz() method is invoked to convert the imported legacy data into xyz format for private, internal use:
define class quadrays as custom
dimension xyzout(3), quadout(4)
procedure quad2xyz(a,b,c,d) && parameters passed from poly object
with this
.xyzout(1) = 1/root2 * (a - b - c + d)
.xyzout(2) = 1/root2 * (a - b + c - d)
.xyzout(3) = 1/root2 * (a + b - c - d)
endwith
endproc
Our polyhedron class definition will accept archival data in either xyz or quadrays format. Note that the edges table requires no conversion, as it references points by the same names, irrespective of format.
Here's what a tetrahedron's 4 vertices look like in quadray format:POINTID ACOORD BCOORD CCOORD DCOORD T1A 1.0000000 0.0000000 0.0000000 0.0000000 T1B 0.0000000 1.0000000 0.0000000 0.0000000 T1C 0.0000000 0.0000000 1.0000000 0.0000000 T1D 0.0000000 0.0000000 0.0000000 1.0000000
A writetable() method, added to Polyhedron, enables us to spit out a snapshot of a shape's internal points table -- before and after a rotation, for example. We take advantage of this method to list out the same tetrahedron's coordinates after they've been converted to xyz using the oQuadrays object:
POINTID XCOORD YCOORD ZCOORD T1A 0.7071068 0.7071068 0.7071068 T1B -0.7071068 -0.7071068 0.7071068 T1C -0.7071068 0.7071068 -0.7071068 T1D 0.7071068 -0.7071068 -0.7071068
On-line Resources:
- Chapters 1, 3, 4, 5, 6 and 7 of this webtext
- Text view of the complete VFP source code
- ZIP file containing the VFP source code, Povray output, data tables, and graphic
- An Introduction to Quadrays
- Other on-line papers demonstrating the VFP + Povray combination
Return to Symbols and Operators
