Using Polyhedra to Teach OOP
and Coordinate Geometry Concepts

Chapter 1:
Designing a Framework

by Kirby Urner
First posted: Oct 24, 1998
Last modified: Aug 25, 1999

Polyhedra may be usefully employed to introduce object oriented programming (OOP) concepts -- because they are objects, after all. Likewise, polyhedra make obvious use of tabulated data, as storage for points and edges. Given that objects consist of data (properties) and operations (methods), we can look at polyhedra as idealized objects.

For example, consider rotation about the X, Y or Z axis as an operation on tabular data. A tetrahedron, a subclass of the more generic polyhedron class, consists of 4 points and 6 edges, tabulated in two tables, one for vertices, the other for edges between the vertices:

  TETPOINTS.DBF

  POINTID                 XCOORD            YCOORD            ZCOORD
  A                     1.000000         -1.000000          1.000000
  B                    -1.000000          1.000000          1.000000
  C                     1.000000          1.000000         -1.000000
  D                    -1.000000         -1.000000         -1.000000

  TETEDGES.DBF

  EDGEID     VERT1    VERT2   
  1          A        B       
  2          A        C       
  3          A        D       
  4          B        C       
  5          B        D       
  6          C        D

When we wish to draw a polyhedron, its writeoutput() method will scan down the list of six edges, and retrieve each of the endpoints (vert1 and vert2) from the Points table, where the xyz coordinates of these vertices are indexed by pointid. For example, edge 5 runs between vertices B and D, so our writeoutput() method will write an instruction telling the computer to draw an edge between (-1,1,1) and (-1,-1,-1) -- the points B and D in xyz form.

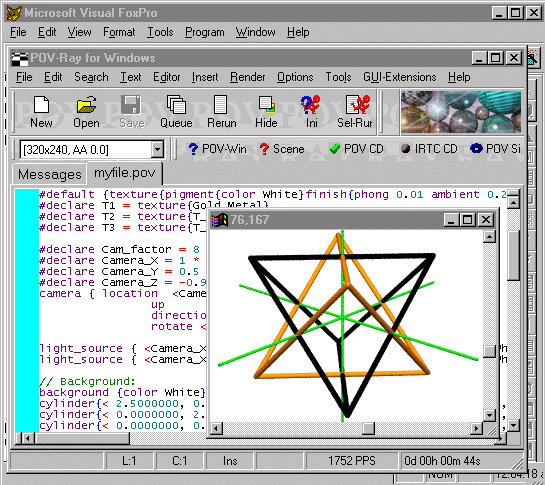
My approach in this demonstration is to exploit the synergetic advantages of using different software packages on their strengths, in combination. We use:

  • Visual FoxPro (VFP), an object oriented dialect of XBase, to do the math, and to write textfile output instructions in a format interpretable by
  • Povray, a free ray tracing and rendering program, to give us our graphical output

The advantages of this approach are several: VFP is very handy with tabular data (such as listed out above), and it implements the OOP model straightforwardly. Povray, on the other hand, takes care of all the messy perspective issues while providing an attractive, finely tunable graphical product.

So in VFP we can concentrate on the OOP and XYZ paradigms and leave the details about how to implement Renaissance-style perspective to Povray.

image

Here's what the writeoutput() method looks like:

    procedure writeoutput
        local x1,y1,z1,x2,y2,z2

        select edges  && select the Edges table
        go top

        scan while not eof()  && scan to the end
            
            =seek(vert1,"points")  && get first vertex
            x1=points.xcoord
            y1=points.ycoord
            z1=points.zcoord
            
            =seek(vert2,"points")  && get second vertex
            x2=points.xcoord
            y2=points.ycoord
            z2=points.zcoord

            this.writepoint(x1,y1,z1)  && nub
        this.writecylinder(x1,y1,z1,x2,y2,z2)  && edge
        this.writepoint(x2,y2,z2)  && nub          
            
        endscan
        return

    endproc

The method goes to the top of the Edges table and scans to the bottom, in this case through 6 records (the edges of the tetrahedron), each time looking up the two vertices, writing a small sphere at each vertex, and a cylinder connecting the two spheres. The spheres provide rounded "nubs" at the ends of our edges, giving the resulting wireframe a smoother appearance, with more "rounded" corners.

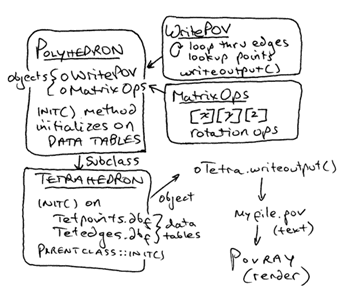
Tying all this together, lets define our Polyhedron class to initialize on some pair of tables (a points table and an edges table). Furthermore, the Polyhedron class imports two additional objects each based on its own class definition:

  • oWritePOV is based on WritePOV, a class which contains methods focused on writing an output file readable by Povray -- such as writeoutput() above,
  • oMatrixOps is based on MatrixOps, and contains the methods for rotating a polyhedron about the X, Y or Z axis (matrix operations).

image

The beginning of the Polyhedron class definition looks like this:

define class polyhedron as custom
    add object oWritePOV as WritePOV
    add object oMatrixOps as MatrixOps
    color  = ""
    degrees = 0
    axis = "X"

Whereas the Polyhedron class definition is not specific about what tables to use for point and edge data, the Tetrahedron subclass is specific, automatically initializing any new Tetrahedron object with data files tetpoints.dbf and tetedges.dbf, open and ready for access:

define class tetrahedron as polyhedron

    procedure init(ptable,etable)
        if parameters()=0
           this.setpoints("tetpoints.dbf")
       this.setedges("tetedges.dbf")
    else
           this.setpoints(ptable)
       this.setedges(etable)
    endif
    * the parent class has code for opening both tables, no
        * matter what their names (always the same aliases), so
        * invoke the parent version of this init() method too
    polyhedron::init()
    endproc

enddefine

When a the rotation method is invoked, the number of degrees (theta) and axis of rotation (X, Y or Z) will already be specified, either by default or passed in as parameters. The relevant matrix operation will be triggered, causing the xyz coordinates of the four points in the data table to change:

    procedure xrotate
        local newx, newy, newz

        *         / 1   0        0       \
        * X AXIS  | 0   cos(a)  -sin(a)  |
        *         \ 0   sin(a)   cos(a)  /

        scan while not eof()
            newx = xcoord
            newy = this.cos_theta*ycoord - this.sin_theta*zcoord
            newz = this.sin_theta*ycoord + this.cos_theta*zcoord
            replace xcoord with newx, ycoord with newy, zcoord with newz
        endscan
        return
    endproc

When the writeoutput() method is next invoked, and same edge table will be used unchanged, but the sphere and cylinder instructions will use the new point data, now altered because of the matrix operation just applied to each of the point table's four records.

The following script uses all of the foregoing class definitions to:

  • create a tetrahedron object, oTetra
  • specify the object's color (orange)
  • have the object write instructions for self-display to a Povray script file
  • set oTetra.color to black
  • rotate the object by 90 degrees around the X axis
  • write to the same script file with more self-display instructions.
* Main sequence -- instantiates objects, sets properties, 
* triggers methods.

close tables

otetra = createobject("tetrahedron")

otetra.setcolor("Orange")
otetra.writeoutput()

otetra.setcolor("Black")
otetra.rotate(90,"X")
otetra.writeoutput()

otetra.rotate(-90,"X")  && set the data table back how it was

release otetra
return

A somewhat more advanced model of the polyhedron class, and its subclasses, will not tie an object such as oTetra, to an external, sharable points table. Rather, when a polyhedron subclass object initializes, it will read its "starting coordinates" to an internal, temporary table, specific to that object. As oTetra gets rotated, only its internal data points will be affected.

According to this implementation, if we subclassed several Tetrahedra, they would all be free to change independently of one another. This enhancement will bring our model much more in line with the true object-oriented paradigm, and will be implemented in Chapter 2.

Also, a more complete implementation of the polyhedron class would include more matrix operations for resizing a shape (scaling), and for sliding it around in space (translating). Indeed, we could use a translation method to improve our rotation method as well, as our rotation matrices work only with reference to the origin (0,0,0).

The standard computer graphics algorithm for letting a shape "rotate in place" no matter where its location, is to:

  • translate the shape to the origin
  • do the rotation
  • translate the shape back to where it came from.

We will implement these resizing and translation methods (along with improved rotation) in Chapter 4. In Chapter 5, we'll implement the whole business all over again, along with some new features, but this time in Java. If you're a native VFP coder, then the Chapter 5 transition to a Java version will likely go smoothly, given the central concepts and application blueprint are common to both versions. In Chapter 6, I drive home the point that many solutions/approaches to the same problems/challenges are possible, especially in a rich and sophisticated programming language. Finally, in Chapter 7, I explore this same application in yet another language, and a very suitable one at that, Python.

On-line Resources:

Return to Main Outline

oregon.gif - 8.3 K
Oregon Curriculum Network