Lecture One:
Naming Numbers
by Kirby Urner
Oregon Curriculum Network
First posted: Sept 11, 2002
Last updated: Oct 10, 2002
First draft posted to mathedcc
So I'm imagining I'm in front of the room with one of those newfangled computer projectors. I'm basically just going to use J in "calculator mode" (interactively, without trying to write programs) to cover some math concepts. Starting with the basics, this lecture focuses mostly on how to name numbers.
I. EXTENDED PRECISION AND RATIONAL NUMBERS
For example, we're maybe used to seeing 3e10 as "exponential notation" for 3.0 * 10^10 (3 followed by 10 zeros). We have the extended precision verb x: to spell that out if we like:
x: 3e10 NB. user's input indented 3 spaces 30000000000
So that sets a precedent for having a letter of the alphabet mixed right in with digits, as part of the "name" or "representation" of a number. Extending that idea gives us other ways of naming. Putting an r between two integers designates a rational number or fraction:
]a =: 1r2 NB. the verb ] causes the value of a to display 1r2 % a NB. % means 'reciprocate' and 1 / 1r2 is 2 2
If we use our extended precision operator (x: ) on a regular integer, J assumes we're asking for the rational equivalent, i.e. x: 2, if reciprocated, gives 1r2 instead of the decimal form 0.5.
% x:2 1r2
This ability to work in rationals is advantageous, e.g. suppose we want to invert a matrix following the text book model of getting fractional results. We define a 3 x 3 matrix using the shape operator ($) with the dimensions specified up front:
] matrix =: 3 3 $ _1 2 5 _8 0 1 _4 3 3 NB. some random matrix _1 2 5 _8 0 1 _4 3 3
Notice how negative numbers are symbolized, using an underbar prefix. This makes the minus sign part of a number's name, separating it from the verb 'to negate' (monadic -).
matrix =: x: matrix NB. I decide to work with rationals...
I could have made matrix rational to begin with. Simply post-fixing an x to any of the entries would have made all the entries rational, as in: matrix =: 3 3 $ _1 2 5 _8 0x 1 _4 3 3
]invmatrix =: %. matrix NB. %. inverts the matrix 3r77 _9r77 _2r77 _20r77 _17r77 39r77 24r77 5r77 _16r77
So I get my answer with fractional elements. Way cool! Notice that the 'invert matrix' verb, %. is mnemonically associated with % -- plain old 'reciprocate'. This is true of J verbs in general: like concepts have like symbolizations, the differences being communicated by "inflecting" a symbol with either . (dot) or : (colon).
As a check on the answer, I can multiply the matrix and the inverse together. In this lecture, we don't need to go into why the phrase below defines matrix multiplication. Take it as a given (e.g. cut and paste it from the phrase book):
mp=: +/ . * NB. defines cayley multiplication matrix mp invmatrix NB. = identity matrix 1 0 0 0 1 0 0 0 1
So we've seen exponential notation (1e10), how to symbolize negative numbers (e.g. 2e_1), how to symbolize rationals (e.g. 1r5), and how to use the extended precision verb to convert numbers to rationals. In sum:
x: 2e_1 NB. express 0.2 as a rational 1r5
Most computer languages stop about here when it comes to representations of numbers. Indeed, many don't include extended precision integers, and many don't work natively with rationals. In doing both, J is already in the minority. But J doesn't stop here. Given we've attached meaning to e, r and _ as part of a number's name, why stop?
II. COMPLEX NUMBERS
Complex numbers come up a lot. J lets us embed the lowercase j to separate the real and imaginary parts. 0j1 is equivalent the i in other notations.
0j1 * 0j1 NB. 2nd root of _1 times itself = _1 _1
We can do basic arithmetic on complex numbers natively, plus we have a host of additional verbs, such as monadic +. to split real and imaginary components into a 2-element array. And + will take the conjugate:
+. 3j2 NB. split into x y 3 2 + 3j2 NB. take the conjugate (negate imaginary part) 3j_2
J includes %: as a monadic square root verb (monadic means it takes one argument on the right). As you would expect, asking for the square root of a negative number returns a complex result:
%:_1 0j1
Using %: dyadically, we can get the nth root of a number:
3 %: 27 NB. 3rd root of 27 3 ]a =: 3 %: _1 NB. 3rd root of _1 (could also go _3^1r2) 0.5j0.866025 a^3 NB. reversing the operation with exponentiation _1
III. SOME SPECIAL IRRATIONALS
It frequently comes up in math that you need x times pi to some power, e.g. 2pi or 1/2 pi^2. J lets you embed the letter p as shorthand for that. 1p1 is just pi. 1p2 is pi to the 2nd power. 1r2p2 is half pi to the 2nd power (returns a floating point). And of course you can use negative numbers on either the left or right.
Combining some of this new knowledge:
x: 0.5p1 NB. return a rational version of 1/2 pi (note r) 1285290289249r818241211368 1285290289249 % 818241211368 NB. convert to division 1.5708 1p1 % 2 NB. compare with pi over 2 1.5708
Similarly, we use Euler's e a lot, in expressions such as 3 e^2. If we use x in place of p (x for exponential), we get similar freedoms:
1x1 NB. e as decimal 2.71828 x: 1x1 6157974361033r2265392166685 NB. rational version 1x_1 NB. 1/e 0.367879
BASES OTHER THAN 10
The letter b gives us the power to work in bases. 2b110 means 110 in base 2.
2b110 6
Now you might think that 2b333 would produce an error, but there's a logical interpretation that applies: 2b333 = (3*2^2) + (3*2^1) + (3*2^0)
(3*2^2) + (3*2^1) + (3*2^0) 21 2b333 21
IV. COMPLEX NUMBERS IN POLAR FORM
Now let's look at what many will consider a trully exotic way of naming a number -- and a complex number at that. Instead of going ajb for a+bj (j means same as sqrt(_1)), we use a polar form, giving magnitude and counter-clockwise rotation around a circle, in either degrees or radians:
1ad90 NB. magnitude 1, 90 degrees, returns j 0j1 1ad1 NB. magnitude 1, 1 degree counter-clockwise 0.999848j0.0174524 +. 1ad_1 NB. x y coords, mag 1, 1 degree clockwise 0.999848 _0.0174524
The verb *. takes a complex number and returns its magnitude and angle, in radians:
*. 0j1 1 1.5708
When we multiply two complex numbers, we multiply their magnitudes, but add their angles of rotation:
c1 =: 3ad30 NB. magnitude 3, 30 degrees around circle
c2 =: 4ad15 NB. magnitude 4, 15 degrees
*. c1*c2 NB. show product as magnitude, angle
12 0.785398
rad2deg =: 180p_1 NB. conversion factor = 180/pi
rad2deg * 1r4p1 NB. testing conversion factor on pi/4
45
rad2deg * 1{ *. c1*c2 NB. convert angle portion of the product
45
In the last line above, we're getting a little fancy. 1{ means "take element 1 from" but indexing is zero-based, meaning we're actually getting the angular figure from the 2-element array returned by *. c1*c2 i.e. 0.785398 (stored to a few more digits of accuracy internally).
We'll conclude this lecture by looking ahead to building longer sentences. Multiplication expects two arguments, is dyadic, but we often want to fix one of these arguments, making a constant multiplier. The bonding verb (&) allows us to convert a dyadic verb into a monadic one by bonding a fixed argument to the left or right.
Since 1ad1 is a complex number that rotates another by 1 degree counter- clockwise, we can build a rotator verb by bonding 1ad1 to * (multiply).
rotate =: 1ad1 & * NB. bond 1ad1 to multiplication operator
rotate 1j0 NB. apply new verb to complex number 1 + 0j
0.999848j0.0174524
rotate rotate 1j0 NB. apply new verb twice
0.999391j0.0348995
rotate rotate rotate 1j0 NB. apply it three times
0.99863j0.052336
*. rotate rotate rotate 1j0 NB. look at magnitude and angle
1 0.0523599
rad2deg * 1{ *. rotate rotate rotate 1j0 NB. convert to degrees
3
V. POWERS OF FUNCTIONS
This thing of applying a verb multiple times is common in mathematics, and is suggestive of powering. The J conjunction ^: -- an inflection of ordinary powering ^ -- lets us specify how many times to keep applying the same verb:
(rotate^:3) 1j0 0.99863j0.052336
Applying it _1 times performs the inverse operation, the same as undoing one application of rotate:
(rotate^:_1) 1j0 0.999848j_0.0174524 rotate (rotate^:_1) 1j0 1
If you want to use several powers in sequence, the right argument to :^ will accommodate this:
rotate^:(0 1 2 3) 1j0 NB. returns sequence of 0,1,2,3 rotations 1 0.999848j0.0174524 0.999391j0.0348995 0.99863j0.052336
The monadic use of i. will generate an array of consecutive integers with the dimensions of its argument, so in place of (0 1 2 3) above, it works to just use i.4:
rotate^:(i.4) 1j0 1 0.999848j0.0174524 0.999391j0.0348995 0.99863j0.052336
This output may now be fed to +. (convert to x y coordinates) or *. (convert to angle magnitude polar coordinates):
+. rotate^:(i.4) 1j0
1 0
0.999848 0.0174524
0.999391 0.0348995
0.99863 0.052336
*. rotate^:(i.4) 1j0
1 0
1 0.0174533
1 0.0349066
1 0.0523599
As a result of applying a verb to an array of complex numbers, we got back a table wherein each row contains the number pair returned by the verb. This is typical J behavior. Assigning the output to a variable would result in a named table permitting further manipulation:
] results =: +. rotate^:(i.6) 1j0
1 0
0.999848 0.0174524
0.999391 0.0348995
0.99863 0.052336
0.997564 0.0697565
0.996195 0.0871557
0 { results NB. take the first row of the results table
1 0
0 {"1 results NB. take first item of every row
1 0.999848 0.999391 0.99863 0.997564 0.996195
1 {"1 results NB. take 2nd column, i.e. y values
0 0.0174524 0.0348995 0.052336 0.0697565 0.0871557
Let's apply powers from 0 to 360 and plot the results. We get fancy again, using multiple assignment to make x and y each take a row of numbers from a 2 x 360 table. Since the results were originally in a 360 x 2 table, I used the transpose verb |: to switch dimensions.
load 'plot' NB. bring in a bunch of canned graphing power 'x y' =: |: +. rotate^:(i.361) 1j0 NB. takes the transpose plot x;y
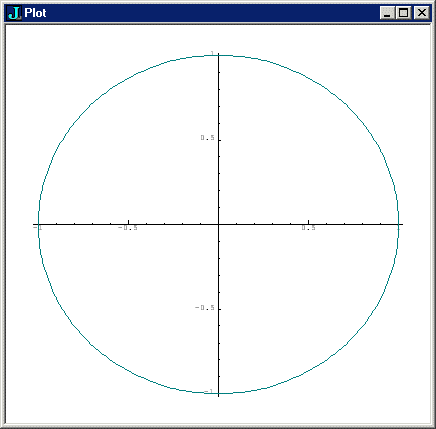
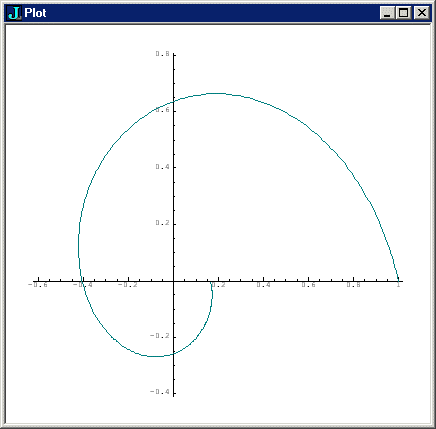
If we make the rotate verb shorten the magnitude a bit with each one degree increment, we get a spiral:
rotate =: 0.995ad1 & * NB. bond new complex number to * 'x y' =: |: +. rotate^:(i.361) 1j0 NB. takes the transpose plot x;y
- Official J website
- Jiving in J
- Introductory J Lectures: [1][2][3][4]
- Trends in Early Math Education