Synergetic Crystallography 101

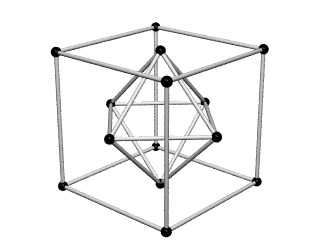
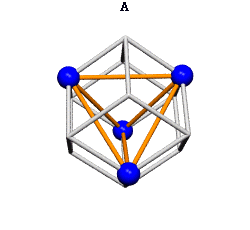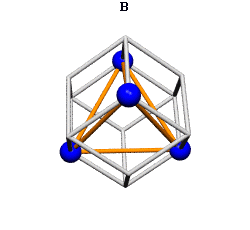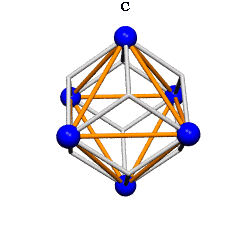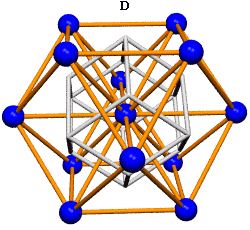
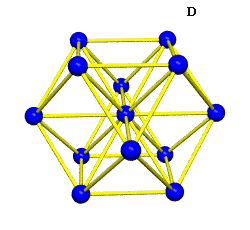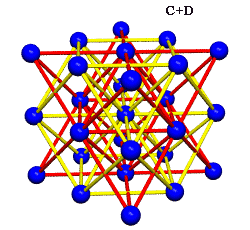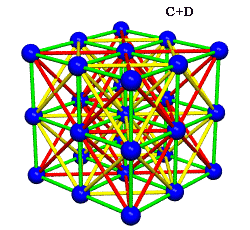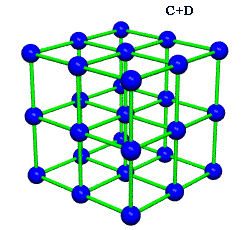
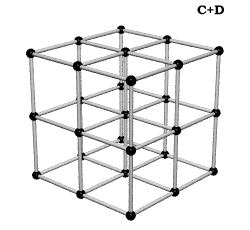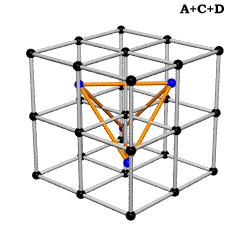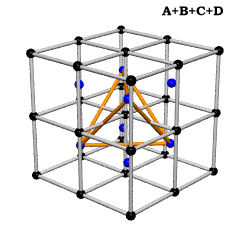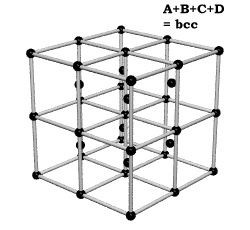
Equating the fcc with the IVM

Crystallography, as traditionally communicated, is inevitably imbued with a strong European bias in favor of making everything cubical or cube-referenced.

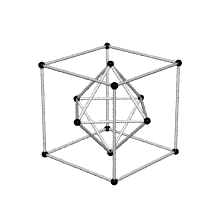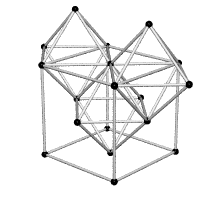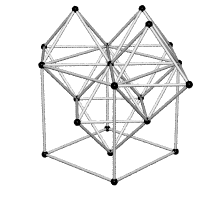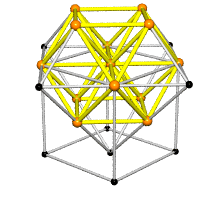
Ergo, the synergetics approach to closest packing of unit-radius spheres as concentric layerings of 10 f² + 2 spheres around a nuclear sphere, in a cuboctahedral conformation, is rarely found in 1900s crystallography books. Rather, we read about the "face centered cubic" lattice (fcc)-- which amounts to the same thing.

To get from the face centered cubic lattice to the isotropic vector matrix (IVM), we need to translate our focus. The graphics below show how the cuboctahedron (shown in yellow) inhabits the same matrix (or lattice) with reference to a nuclear position. Packing outwardly from this nucleus in cuboctahedral conformation is another way to generate all the same fcc loci (positions).

Mapping crystal structures in a 4 IVM framework

The isotropic vector matrix defines tetrahedral and octahedral voids, which may in turn be occupied by alternate IVMs. The tetrahedral voids define two alternate IVMs, and the octahedral voids a complement to the currently active one -- for a total of 4 IVMs in all. By selecting combinations of these interpenetrating IVMs, we define some of the lattices typically encountered by crystallographers.

The rhombic dodecahedron provides a useful reference system for anchoring all four IVMs to a single shape.[1] The short diagonals of the rhombic faces terminate in tetrahedral voids, while the long diagonals terminate in the octahedral voids.

In this paper, I am using Russell Kasman-Chu's nomenclature, identifying the 4 IVMs as compementary pairs: A and B, C and D.[2] These are shown in the animated GIF at right.

Each pair of IVMs is equivalent to the simple cubic lattice, and these two lattices interpenetrate to define the body-centered cubic lattice.

In the graphic below we see IVMs C + D combining to form a simple cubic lattice.

Note that the IVMs serve to position the lattice points, at which point the specific chemistries will determine the actual bonding configurations of the atoms in question. The purpose of the 4 IVMs framework is to suggest a convenient schema for categorizing various commonly encountered lattices. See Kasman-Chu's paper for more details.

The body-centered cubic lattice (bcc) is derived from 2 inter-penetrating simple cubic lattices i.e. starting with (C+D) as shown above, we add IVMs (A+B):

VRML views

• fcc with octas and cubocta
• simple cubic lattice (no frills)
• bcc with embedded tetrahedron

Notes:

[1] Fuller uses this approach in Synergetics in his discussions of Coupler axes interconnecting IVM sphere centers and inter-spheric voids ( 954.40, 954.70).

[2] The ccp and hcp family of structures derived from interpenetrating lattices by Russell Kasman-Chu

For further reading

• Dr. Arthur Loeb. Contribution to Synergetics (1st print volume, Macmillan)
• Interpreting crystal structures with synergetic geometry by Scott Childs
• Alexander Graham Bell and the Octet-truss
• Picture of K. Urner with R. Kasman-Chu (Sept 11, 1993)
• Beyond Flatland: Geometry for the 21st Century
• Studies in Sphere Packing
• Morphology of the Virus
• Java source code for supplying the graphics and VRML views used in this paper (downloadable version may lag capabilities of inhouse prototype)
• Another approach to doing graphics using Python
• Readings on Synergetics

Collaborative Projects

---

A Mathematical Canvas