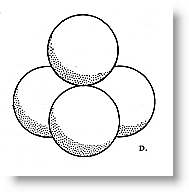
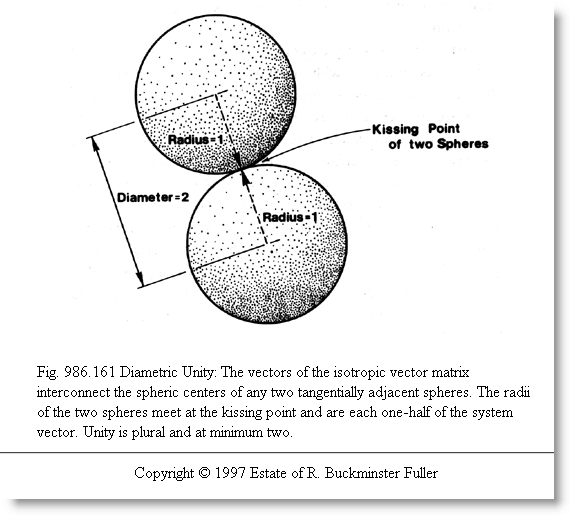
Martian Math inherits from the pioneering studies of R. Buckminster Fuller in making use of "tetrahedral mensuration" meaning a regular tetrahedron serves as a unit of volume.

The centers of tangent unit-radius balls define the vertexes of this unit, as shown above.

Having a tetrahedron serve as unit volume means any positive integer N to the 3rd power is modeled by a corresponding tetrahedron of edges N.

Integers relate to the "frequency" concept (as distinct from "angle"), a subdividing along each edge with a corresponding carving up of the tetrahedron into smaller volumes.

The internal skeleton so formed was dubbed the "isotropic vector matrix" (IVM) by Fuller and is known in chemistry as the "face-centered cubic lattice" (FCC), and in mathematics as the "cubic closest packing" arrangement (CCP).

Alexander Graham Bell also did pioneering studies with this space frame, also known in architecture as the "octet truss" (per Fuller's patent).

Having students connect these dots, despite the various nomenclatures or shop talks (namespaces) is one of the goals of this particular curriculum.

In a sphere packing context, each interval is a sphere diameter in length and represents a connector between adjacent ball centers.

Given the balls may be accounted as unit radius (or 1/2 a diameter), the tetrahedron so formed may be accounted as having face diagonals of 2.

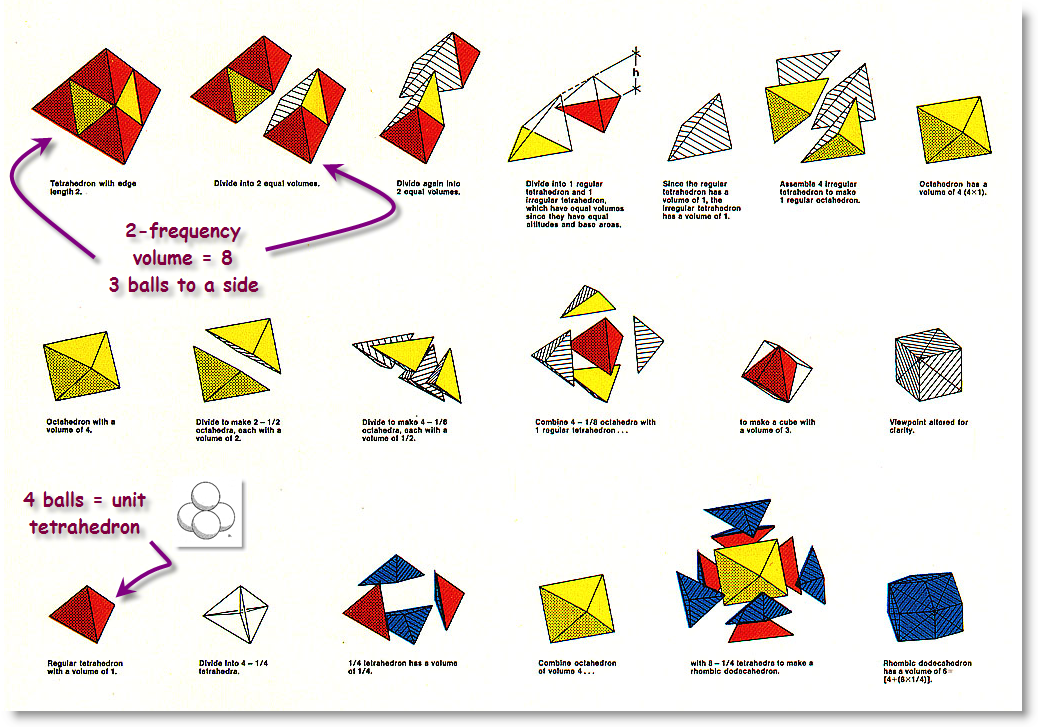
The cube depicted above contains an inscribed unit volume tetrahedron of edges 2 R i.e. this is the control length connecting adjacent sphere centers, is 1 diameter.

In the color sequence below, the red tetrahedron (see start of 3rd row) is our unit of volume, as defined by six intervals of length 2R (1D).

The tetrahedron in the first row has edges 2D and would take 10 unit-radius spheres to build. This is a 2-frequency tetrahedron.

The XYZ space-filling cube, conventionally our unit of volume in Earthling Math, is depicted in blue in the graphic below.

The red cube is our volume 3 in the synergetics "concentric hierarchy" while the purple tetrahedron it contains is volume 1.

One ball of unit-radius R is shown for context. Four of them in intertangency would take us back to the top graphic on this page.

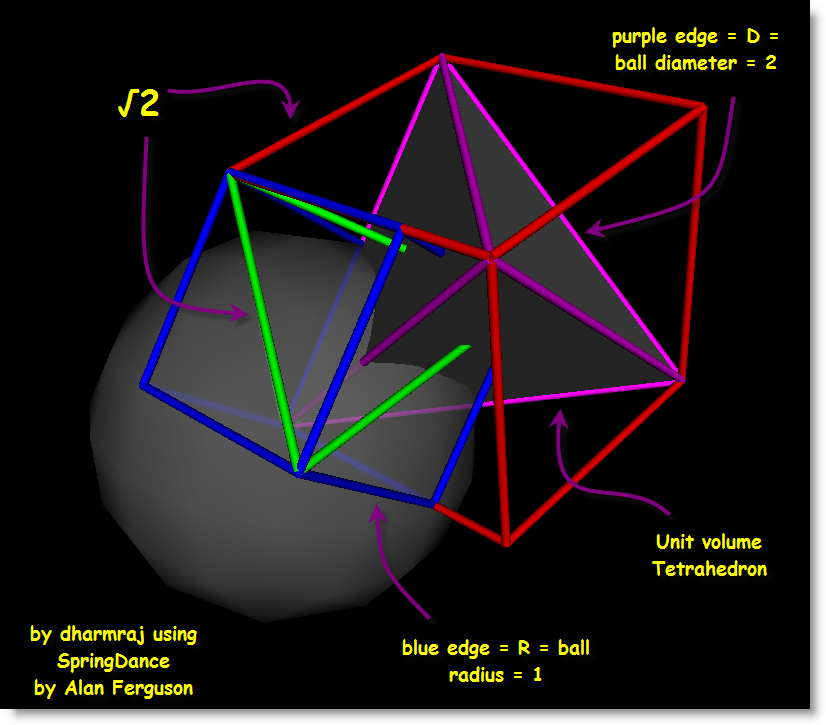
Clearly the Earthlings would not agree that the red cube (above) could have a volume of three.

The blue cube of edges one, would be considered the XYZ unit of volume, not the purple tetrahedron (their volumes differ by about 6%).

This is because in XYZ thinking (Earthling Math), we have a different model of 3rd powering than we have in Martian Math.

A conversion constant may be used to derive the Martian volume for any shape, given its XYZ volume as input.

For example, the red cube above, in XYZ terms, would have a volume of approximately 2.828427.

The conversion constant, or S3, is about 1.06066.

1.06066 times 2.828427 gives us ~3.0, the "Martian volume" we expect from our Martian volumes table below.