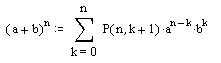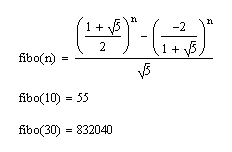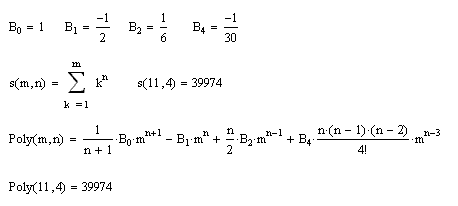1: Getting Serious About Series
by Kirby Urner
First posted: Feb 13, 2000
Last modified: Jan 7, 2003
One hallmark of the Oregon Curriculum Network approach is its focus on spatial geometry. For example, in this essay, I emphasize the following math facts:
- various number series correspond to specific sphere packing arrangements
- a square number is the sum of two consecutive triangular numbers
- the sum of consecutive icosahedral shell numbers is a cuboctahedral number
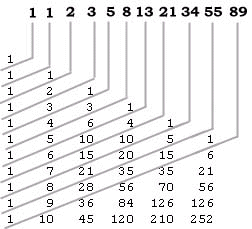
- triangular, square, and tetrahedral numbers show up in Pascal's Triangle
- Pascal's Triangle connects to the golden ratio (phi) via the Fibonacci numbers
- the golden rectangle is embedded in the icosahedron
Given this geometric focus, students will naturally want to do some modeling. Hands-on projects will of course require supplies of various kinds:
- in-house or store-bought items (marbles, glue, card board, tape...)
- commercial kits (e.g. ZomeTools, Roger's Connection)
- other specialized (and more expensive) products (e.g from Design Science Toys)
When it comes to computer graphics, we also need to supply some hardware and software tools. One promising approach (the one used in this essay) is to harness the combined power of:
- Python, a free, cross-platform computer language with development environment
- Povray, a free, cross-platform ray tracing package, plus scripting language
- HTML, a cross-platform markup language for making text and graphics browsable
 Python is
not confined to performing in a graphics-related role in this
curriculum, but serves as a general purpose workhorse. Python
notation provides an alternative, human-readable syntax for various
core algorithms (some going back hundreds or even thousands of
years), thereby capturing the whole idea of "rules" and "rule
following" (using Wittgenstein's terminology) -- with the computer
(not the student-programmer) in the role of "mindless rule
follower".
Python is
not confined to performing in a graphics-related role in this
curriculum, but serves as a general purpose workhorse. Python
notation provides an alternative, human-readable syntax for various
core algorithms (some going back hundreds or even thousands of
years), thereby capturing the whole idea of "rules" and "rule
following" (using Wittgenstein's terminology) -- with the computer
(not the student-programmer) in the role of "mindless rule
follower".
By supplementing conventional, pre-computer math notations with a very high level language (VHLL), we give students access to complementary modes of encoding rules. The hope is that students will learn to write programs as a means to test and refine their understanding of math concepts -- will look at programs as "math poems" (or as attempts toward this ideal).
The Python language (named for Monty Python, the British comedy troupe -- although the snake connotation gets some air play as well) is vastly more comprehensible to human readers than most other languages (e.g. C/C++), plus it provides an interactive, responsive environment giving students fast, positive reinforcement for correct usage.
For example, here's a simple rule for generating the triangular numbers:
def tri(n):
# triangular num n
# = sum of n consecutive counting nos (n>=1)
if n<=1: return n
else: return n + tri(n-1)
The above rule, or function definition (def) returns the nth triangular number, and is defined recursively, meaning it calls itself repeatedly, until done.
And here's what it looks like to use this, and related functions, at the interactive command line:
Python 1.5.2 (#0, Apr 13 1999, 10:51:12) [MSC 32 bit (Intel)] on win32 Copyright 1991-1995 Stichting Mathematisch Centrum, Amsterdam IDLE 0.5 -- press F1 for help >>> import series >>> series.tri(10) 55 >>> series.sqr(5) 25 >>> series.tetra(6) 56 >>> series.fibo(10) # the L identifies a "long integer" (potentially huge) 55L

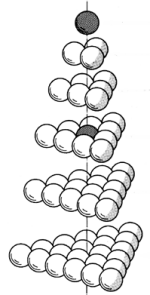


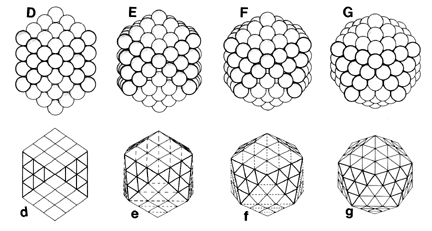
 The sphere packings depicted
above (top row) go from a cuboctahedral to an icosahedral
conformation as we move from left to right. Beneath the sphere
packings, we see the same transformation using edges and vertices
-- the vertices correspond to the spheres in the row above. The
number of spheres (or vertices) remains unchanged as we move from D
(d) to G (g). This transformation is a phase of what Fuller dubbed
"the jitterbug".
The sphere packings depicted
above (top row) go from a cuboctahedral to an icosahedral
conformation as we move from left to right. Beneath the sphere
packings, we see the same transformation using edges and vertices
-- the vertices correspond to the spheres in the row above. The
number of spheres (or vertices) remains unchanged as we move from D
(d) to G (g). This transformation is a phase of what Fuller dubbed
"the jitterbug".