Vpython + Synergetics
First posted: October 23, 2006
Last Modified: October 24, 2006
Synergetic geometry, pioneered by the late American Transcendentalist R. Buckminster Fuller, is centered around a volumetric hierarchy of concentric polyhedra.
Two expansive/contractive transformations, a positive and negative, or left and right, are anchored on either side of cosmic zero, the origin. This "bow tie Universe" is the aconceptual context.
The transformations, modeled by the so-called jitterbug, involve expanding outward from nothing to a volume 24 cube, then squeezing back down to zero, before exploding outwardly again, this time in a "through the looking glass" context.

Fig: 1: animated GIF of the concentric hierarchy by Kirby Urner
Fuller anchored this whole show to the unit-volumed tetrahedron early on, creating one in each Universe (the tuned in and the tuned out, with respect to some me-ball observer), and having them intersect as the "duo-tet cube" of volume 3.
In traditional cubes-based XYZ mathematics, this wouldn't be a volume 3 cube, as the edges are 2nd root of two, but synergetics most primitively models 3rd powering as a growing/shrinking tetrahedron, not as a size-changing cube. A conversion constant may come in handy, the 2nd root of 9/8, but we needn't get into that here (see below for further reading).
The next bigger whole number volume Bucky wrote about a lot tended to be the octahedron of volume four, dual to the volume 3 cube, and inscribed in the same rhombic dodecahedron as long face diagonals (the cube is made of its short diagonals). This diamond faced dodecahedron has a volume of precisely 6 relative to our unit of volume.
1, 3, 4, 5 (see below), 6... So where in this picture is a polyhedron of volume 2? Surely there is one.
In the second volume of the original work, published by Macmillan, Fuller gets more deeply into the rotationally five-fold symmetric polyhedra, including their dissection into a small set of modules. Some of the recursive properties of the T-module were definitely on his radar, but later insights, obtained by David Koski, merited a Synergetics Explorer Award for an original contribution (I got one too, for other accomplishments).
Among David's insights, achieved using a phi-based place value system, modelable as T-modules stepped up and down the phi scale, was the relationship of the rhombic triacontrahedron to many other shapes, including the lowly unstable cube (affectionately: "qyoob").
Given the concentric hierarchy's already-established icosahedron of approximate volume 18.51, reached through a jitterbug transformation on the cuboctahedron of volume 20 (defined by 12-around-1 CCP unit-radius spheres and inscribed in a 2-frequency volume 24 cube), we have its dual, the pentagonal dodecahedron, intersecting at 30 mid-edges, and defining the 30 facets of the rhombic triacontahedron, as depicted below.
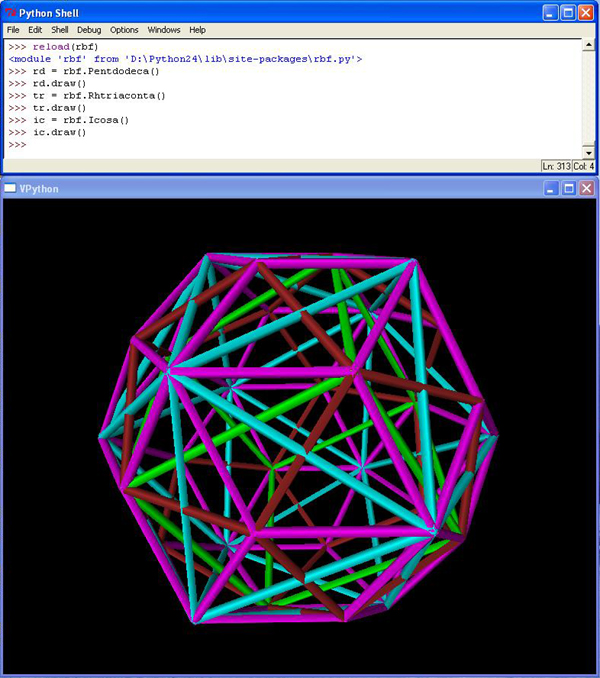
Fig: 2: using vpython
to visualize the concentric hierarchy
An interesting result of computation is that the green cube in the above picture has precisely two fifths the volume of the encasing rhombic triacontahedron. Since Fuller's concentric hierarchy already contains such a shape of precisely volume five, we now have a good candidate to fill the volume two position: the cube inscribed in its pentagonal dodecahedron, as twelve face diagonals (yes, more than one cube fits this description, five do -- all of the same volume two).
Note that if the cyan icosahedron in the above graphic is the one obtained from the volume 20 cuboctahedron by jitterbugging, then this green cube is not the volume two cube I've been talking about.
No, we first need to shrink the outermost rhombic triacontahedron by 1/phi. This makes it fit snugly around a CCP ball at the center (faces tangent thereto), just like the volume 6 rhombic dodecahedron does. Then we need to shrink it just a tad more, turning 120 E modules into 120 T modules each of volume 1/24.
Apply these same scale factors to the green cube, and you've reached our volume 2 goal, depicted again in green (my usual "qyoob color") below.
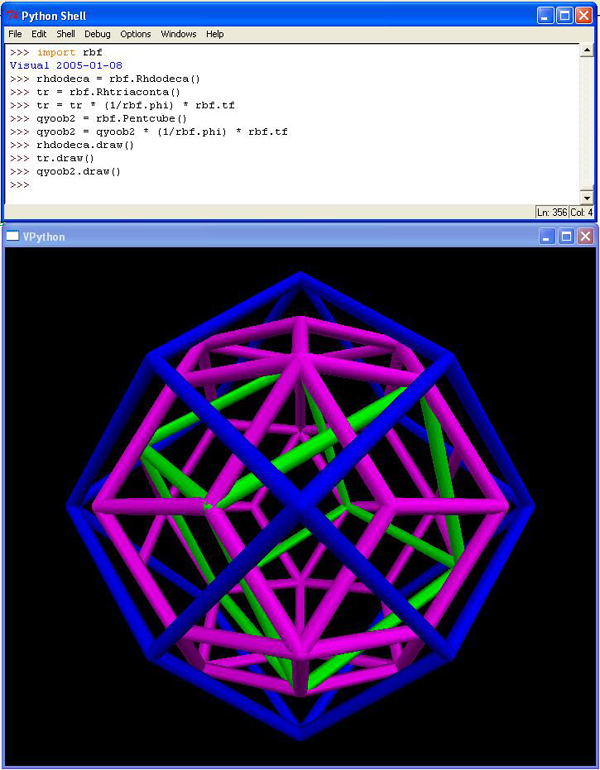
Fig. 3: spheric with volume 5 triacontahedron & volume 2 cube
The final scaling factor, tf, is 0.99948333226234343 in Python, and so the final adjustment is relatively minor, yet plenty real. In Synergetics, it models a very thin line between tuned out and tuned in, but let's save that story for another day.
For further reading:
- Synergetic Hierarchy of Concentric Volumes
- related posting on Synergeo (a Yahoo! eGroup)
- David Koski: Playing with Blocks -- blog posting
- Some scribbles by David Koski (Bridgeport Ale House, Hawthorne District, Oct 23, 2006)
- Practicing MultiCulturalism (blog posting re the synergetics constant)
- Talk About T-Modules (posting to Math Forum, Oct 24, 2006)
- VPython
